Everlasting Options
May 11, 2021 | Dave White, Sam Bankman-Fried
Contents
Introduction
This paper introduces a new type of derivative, the everlasting option. Everlasting options give traders long-term options exposure without the effort, risk, or expense of rolling positions. We derive a simple no-arbitrage pricing model for everlasting options which extends to all funding-fee-based perpetual derivatives, including perpetual futures.
Options Basics
Option Types
We'll start by providing a brief overview of the simplest type of option, the European option. There are two types of European options, calls and puts.
A call gives the holder the right to buy a certain asset (the underlier) for a certain price (the strike), at a certain time on a certain date (the expiration).
A put gives the holder the right to sell the underlier for the strike price at expiration.
Examples
For example, a $3000 strike May 15 ETH put gives the holder the right to sell 1 ETH for $3000 at a particular time on May 15.
If the trading price of ETH (the spot) is $2900 on May 15 when the put expires, the trader will be able to buy 1 ETH for $2900 on the market and then immediately sell it for $3000 via the put, locking in a profit of $100. This quantity is known as the payoff.
On the other hand, if the trader is holding a $3000 strike put at expiry when the price of ETH is $3100, the trader can sell ETH for a higher price on the market than she can using the put. In this case, there is no way to profit using the put, and we say the payoff is $0.
Payoff Calculation
Although a European option can only be used, or exercised, at one specific moment on its expiration date, we can calculate the payoff at any time. It is a measure of how much money the option would be worth if it were to be exercised immediately.
In general, the payoff of a put is max(strike-spot, 0). The farther below the strike price ETH is trading, the more money we can make selling ETH via the put. But, if the price of ETH is above the strike price at expiration, then it is better to sell ETH directly on the market than it is to use the put, and the put is worthless.
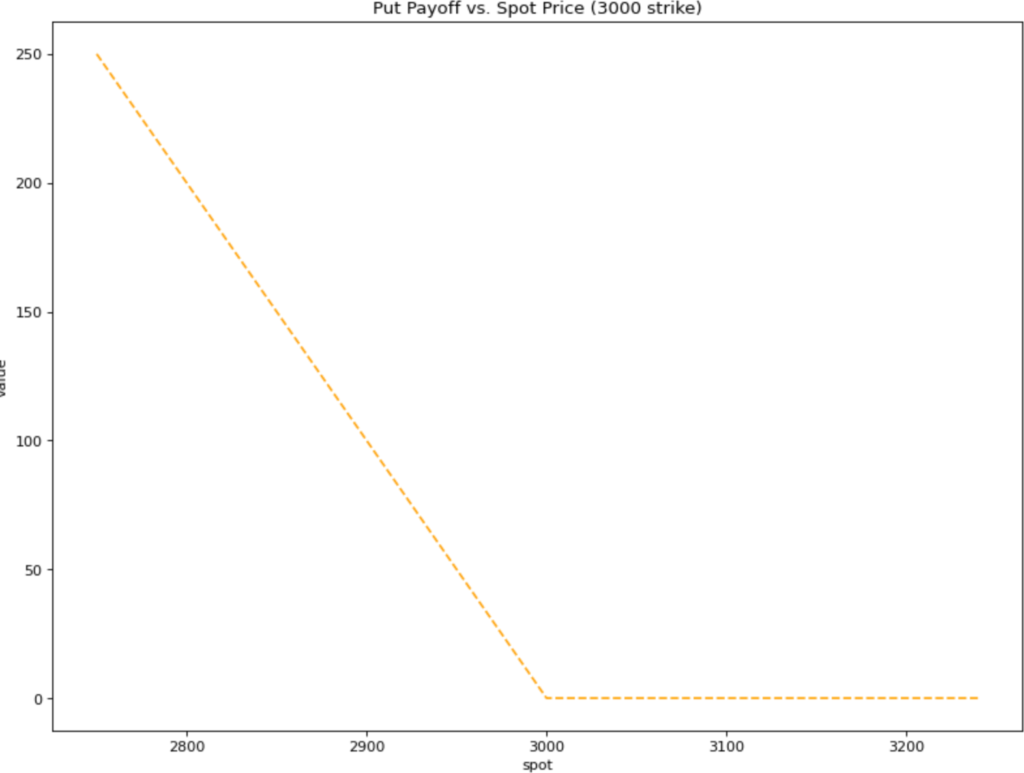
Similarly, the payoff of a call is max(spot - strike, 0). If ETH is trading at $3100 and we have a $3000 strike ETH call at expiration, we can buy ETH for $3000 using the call and then immediately sell it on the market for $3100, netting a payoff of $100. But if ETH is trading at $2900 and we have a $3000 strike ETH call, the payoff is $0.
Options Pricing
An option is generally worth more than its payoff up until the moment it expires (excluding a few special cases).
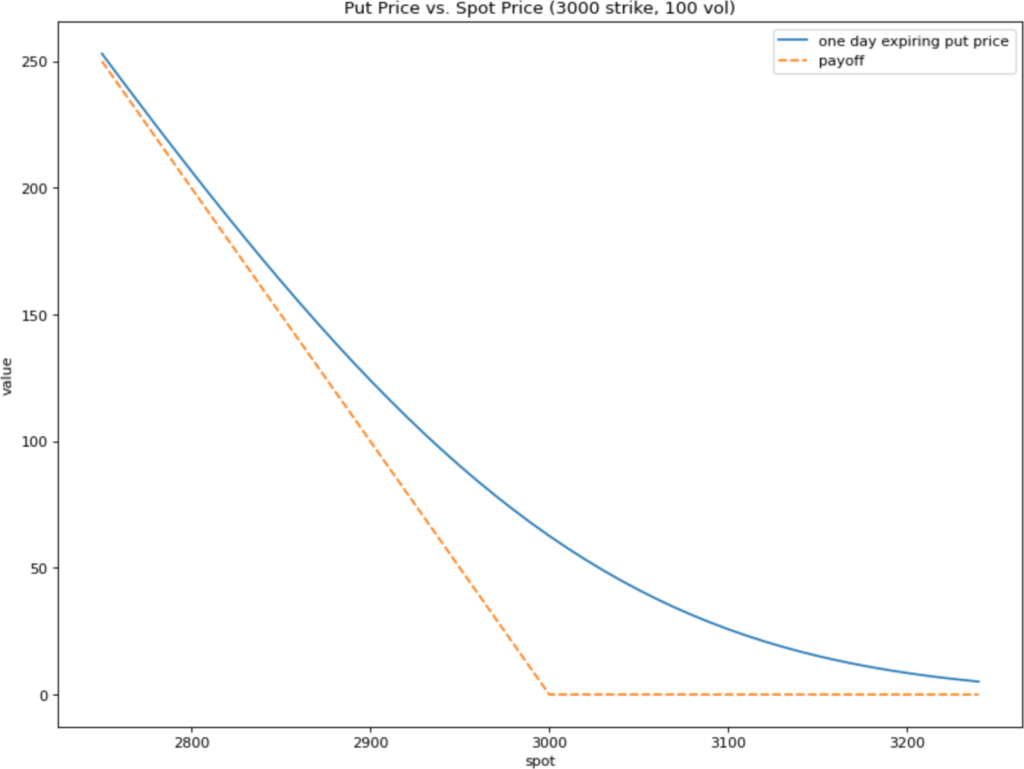
Consider the $3000 strike ETH put expiring tomorrow. If the price of ETH is currently $3000, this put's current payoff is $0. But the price of ETH could fall by tomorrow, in which case the put would be worth more than $0 at expiry. So the put must be worth something greater than $0 now to account for that possibility.
One basic and widely-used model for options pricing is the Black-Scholes model. The graph below shows the Black-Scholes price of a $3000 strike ETH put compared to the payoff at various spot ETH prices one day before expiry.
Rolling Positions
Definition
A primary use case for options is hedging, or protecting against risk. If an investor holds a large portfolio of ETH, for example, she may choose to buy enough $3000 strike ETH puts to ensure that she will always be able to sell her position for at least $3000 per ETH, regardless of what happens to the market price of ETH.
However, these puts will eventually expire. If the investor wants to keep her hedge, she will have to roll her options position. In this case, this means closing out the position in the puts that are about to expire and opening a new position in puts with the same strike that will expire later.
Example
For example, the investor might have originally bought $3000 strike May 15 ETH puts. When they get close to expiring on May 15, she may sell them and buy the same number of $3000 strike June 15 ETH puts. She will have to repeat this process every month for as long as she wants to hold her position.
Problems
When the investor comes to the market to roll her position, she will most likely be trading with a market participant called a market maker.
Market makers make money when uninformed participants — such as those rolling options positions — trade against them. However, market makers lose money when informed participants — such as those who know news about the price of ETH — trade against them.
Because market makers don't know who is informed and who is uninformed, they must charge a fee, called a spread, on every trade. Spreads tend to be especially high in the options market, where informed trades can be very costly for market makers. This makes rolling positions a costly proposition.
Rolling a position also involves work and risk. The trader may simply forget to roll, leaving her position unhedged. Or she might misclick, or execute the trade incorrectly, which can be expensive and dangerous. Even if everything goes perfectly, the whole process is stressful and takes time, siphoning attention away from more productive endeavors.
Existing Solutions
There is an existing product called the perpetual American option, which is an option that can be exercised at any time and has no expiration date. Selling a perpetual American option requires a market maker to take on a huge amount of risk and uncertainty up-front, which makes them both very expensive and very difficult to price. As a result, they are effectively never traded. The existence of this product is why we call our new alternative the everlasting option.
Liquidity Fragmentation
The existence of many different options expiration dates leads to one additional problem: liquidity fragmentation. If market makers must make markets on options expiring not just this week, but every week for the next three months, they will be forced to spread out their capital, making it harder for other participants to execute large trades or to determine fair prices. This fragmented market also makes trading options more confusing, as participants must decide which expiry to transact in.
Analogy to the Futures Market
Futures contracts, which traditionally have expiration dates as well, share all of these problems.
If a trader wants long-term exposure to ETH using traditional expiring futures, she will have to roll her position just as she would in the case of options. For example, she might buy the ETH futures contract expiring May 15. Then, close to expiry on May 15, she might sell that contract and buy the ETH futures contract expiring June 15, and so on.
Just as with options, rolling her futures position takes time, introduces risk, and will require her to pay spreads to market makers on an ongoing basis. The existence of multiple futures expiries also leads to liquidity fragmentation in the futures market.
Perpetual Futures
Perpetual Futures ("perps" for short), introduced to crypto by BitMEX in 2016, solve these problems. They give traders futures exposure for as long as they want it without the need to roll. They also concentrate all the futures liquidity for a given underlier on a given exchange into a single product.
Perps have become massively popular, trading tens and sometimes hundreds of billions of dollars of value per day.
Mechanism
Simplified a bit, perps work as follows: every day, those who are long the perp (have bought it) must pay a funding fee to those who are short the perp (have sold it).
This funding fee is calculated as (mark-index): the difference between the mark price, the trading price of the perp, and the index price, the price of the underlier, such as ETH.
This funding fee mechanism causes the price of the perp to stay in line with the price of the underlier. Roughly speaking, if the perp gets much more expensive than the underlier, then longs will have to pay high funding fees, which should incentivize them to sell the perp, bringing down its price.
As it turns out, we can get a lot more precise than this. See The Cartoon Guide to Perps for a walkthrough of perp mechanics, or our model below for a precise valuation formula.
Examples
If the ETH perp is trading at $3100 while the price of ETH is at $3000, the longs must pay the shorts mark - index = $3100 - $3000 = $100 per day.
If the ETH perp is trading for $2900 while the price of ETH is at $3000, mark - index = $2900 - $3000 = -$100, meaning the shorts must pay the longs $100 per day.
Everlasting Options
Everlasting options are the equivalent of perpetual futures for options.
A trader holding the $3000 strike everlasting ETH put can effectively always sell her ETH for $3000. She will have to pay funding fees to finance her position, but because she does not have to trade with market makers on an ongoing basis, she does not pay spreads or incur operational risk except when entering and exiting her position.
Since multiple expiries are no longer required, liquidity will be less fragmented, although in the basic version there will still be different everlasting options for different strikes.
Mechanism
Everlasting options work exactly the same way as perpetual futures, with one difference: the funding fee is calculated as the difference of the mark price and the current payoff of the option, so that the funding fee is (mark - payoff) instead of (mark - index).
Examples
Consider the $3000 strike everlasting ETH put with funding paid once daily.
If ETH is currently trading at $2900, the current payoff of the put is $3000 - $2900 = $100. If the everlasting put is trading for $150 the instant before funding is paid, then the longs would have to pay the shorts mark - payoff = $150 - $100 = $50 per day.
If ETH is currently trading at $3100, above the strike of the everlasting put, then the put's payoff is $0. If the everlasting put is trading for $50 the instant before funding is paid, then the longs would have to pay the shorts mark - payoff = $50 - $0 = $50 per day.
Notice that the payoff of a $0 strike ETH call is just the price of ETH — in other words, payoff = index. This means the $0 strike call is equivalent to an ETH future. Appropriately, the daily funding fee for the $0 strike everlasting call is mark - payoff = mark - index, the same as the funding fee for a perpetual future.
Pricing
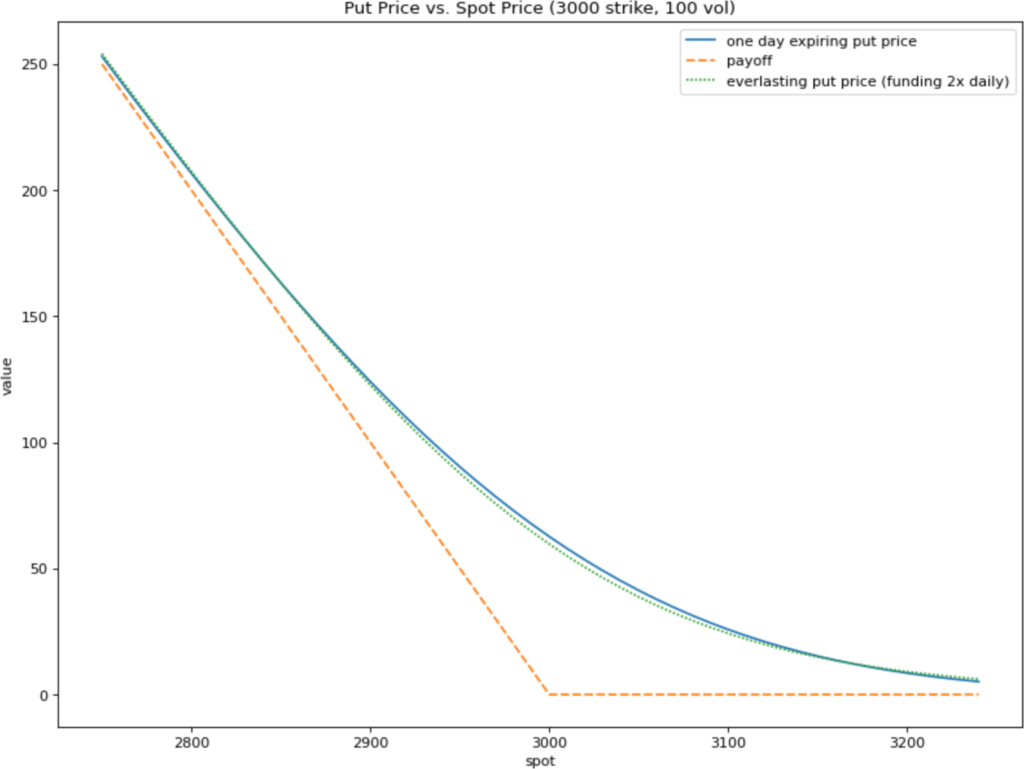
Everlasting options would not be very useful if we didn't know how much they were worth. Fortunately, by means of the no-arbitrage argument laid out below, we do: they are equivalent to a particular constantly rolling options portfolio, and will therefore have the same price as that portfolio. If these prices diverge too much, arbitrageurs will step in to bring them back in line.
If funding is paid once per day, this equivalent portfolio consists of one half an options contract expiring today, one quarter of an options contract expiring tomorrow, one eighth of an options contract expiring the day after that, and so on. All of these contracts have the same strike as the everlasting option itself.
We can also create an everlasting option with multiple smaller funding payments per period -- i.e. 1/24 of the funding is paid each hour -- which changes the composition of the equivalent portfolio. See Appendix B of https://www.paradigm.xyz/static/everlasting_options.pdf for details.
In either case, we can price the everlasting option by pricing this basket. This can be done simply by taking the weighted sum of the individual options prices (estimating the contribution of positions consisting of less than, say, 1/1024 of the portfolio). Options market makers are quite capable of pricing these individual expiring options.
If we were to use simple Black-Scholes assumptions, which do not match real world behavior but are close, an everlasting option with funding paid twice daily would behave almost exactly like a regular expiring option with the same strike expiring in one day.
Equivalent Portfolio
Price Dynamics Around Funding Payment
Reasoning about funding-fee-based perpetuals such as everlasting options is tricky because their pricing contains a natural discontinuity. Funding is paid at a particular, precise time, say, midnight. Just as is the case when stocks pay a dividend, we should expect the price of the perpetual to jump immediately after funding payment.
Therefore, while it is natural to think of things happening "at the same time as" the funding payment is made, this will only lead to suffering. When reasoning about the behavior of a perpetual derivative around funding payment time, it is best to think about what happens either immediately before, or immediately after, funding is paid.
As an aside, to the extent that current perp exchanges do not automatically update their order books after funding payments, as stock exchanges do after dividends, they are exposing their market markers to arbitrage losses. For example, if the longs are due to pay the shorts a funding fee, a rational trader should short the perpetual a microsecond before expiry, collect the payment, and then buy to close their short a microsecond after expiry, collecting a profit with little risk.
Equivalent Portfolio Intuition
Description
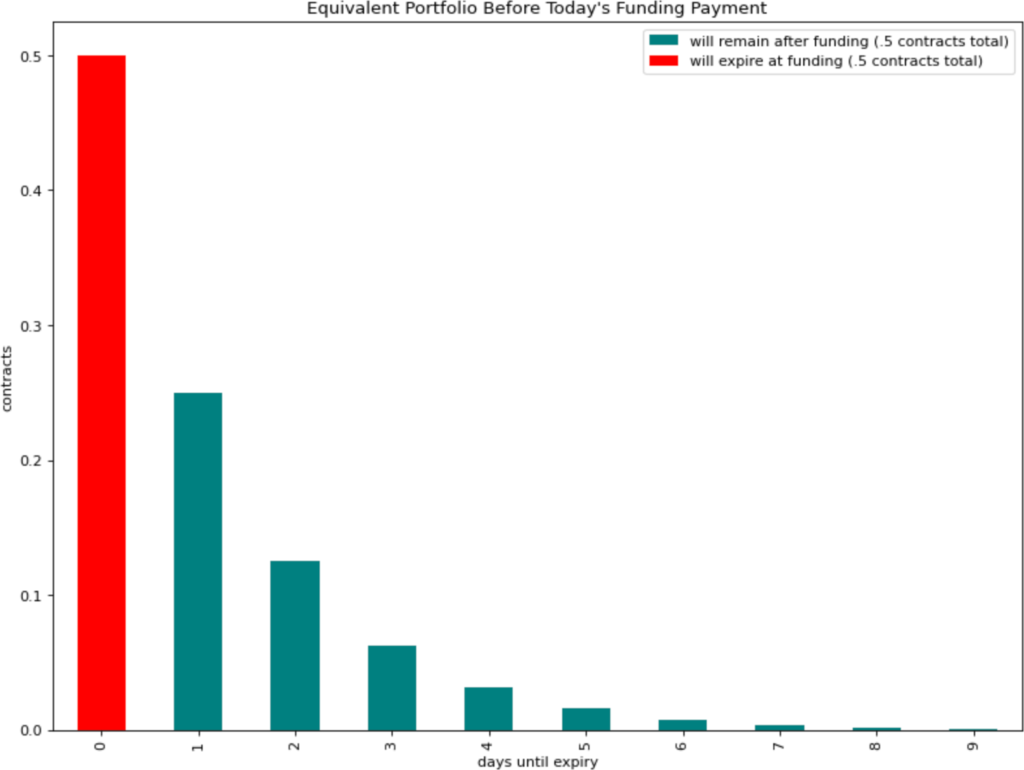
As mentioned, an everlasting option for which funding is paid once daily is equivalent to a portfolio of regular expiring options: one half of a contract expiring at the time of the next funding payment, one quarter of a contract expiring at the time of the funding payment after that, one eighth of a contract expiring at the time of the funding payment after that, and so on. The total number of contracts in this portfolio sums to one.
This means that, at the time of the funding payment, half of a contract, representing one half of the total portfolio, has just expired. The funding payment then corresponds to the cost of rolling the portfolio: buying half a contract's worth of new options to make up for the half contract that has just expired. But, unlike in the case of manual rolling, these new contracts are distributed across multiple expiries, no spreads have to be paid, and no execution risk is incurred.
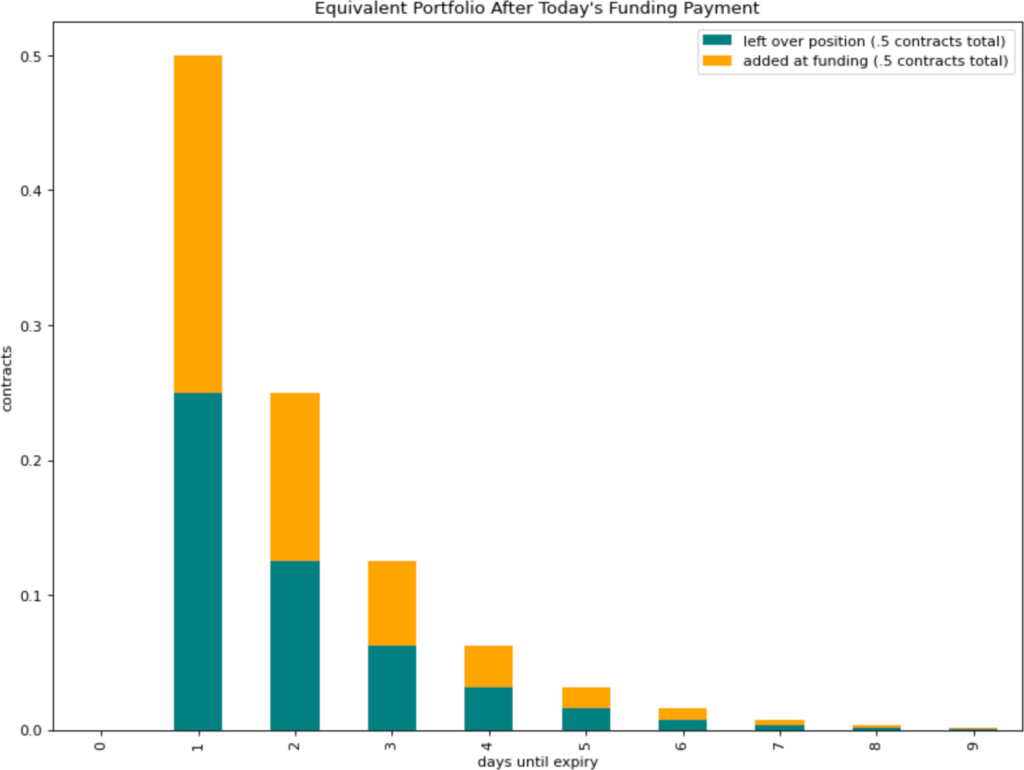
Argument
Imagine Alice is long one contract of an everlasting option for which funding is paid once daily, at midnight.
Alice must pay (mark - payoff) in funding tonight at midnight. Let's think about what this cash flow means. The mark price is the cost to buy the everlasting option infinitesimally before funding is paid, so Alice pays what she has to to double her position. On the other hand, since the term for the payoff is negative, she receives the payoff, which is what she would get if she were long one contract of the equivalent regular option expiring at midnight.
To repeat, if being long an everlasting option is equivalent to being long some portfolio of regular options, this means Alice doubles her position in each of those options an instant before expiry, then receives one contract's worth of payoff at the instant of expiry. That would imply that, up until she doubles her position, Alice is long exactly half a contract of the option expiring tonight at midnight.
Extending this train of thought, if we want Alice's everlasting option equivalent portfolio to keep working after tonight, her position in the regular option expiring midnight tomorrow must be exactly half of a contract after the doubling tonight. This can only be the case if it it is one fourth of a contract before the doubling... and so on.
Note this argument works for any expiring derivative with a defined payoff, not just European options.
Formal Proof
See Appendix B of https://www.paradigm.xyz/static/everlasting_options.pdf.
Further Applications
This framework can be used to price any funding-fee based perpetual derivative for which we can price the expiring equivalents, not just European calls and puts. That includes perpetual futures.
It also includes binary puts, which pay off $0 if the price of the underlier is above a given strike and $1 if it is below, and can therefore be used as proxies for protocol failure.
Floating Strike Everlasting Options
The framework can also be used to price a perpetual option whose strike is an exponentially-weighted moving average of the underlier price over time. This is because the expiring equivalent, the floating-strike Asian option, can also be priced, although doing so is not simple.
Owning such a put would effectively always allow an ETH holder to sell their holdings at, say, the exponentially-weighted average price of ETH with a half-life of one day, protecting her against sudden drops in the price of ETH.
Because the strike would automatically follow the price of ETH, it is possible that a single such product could fulfill the hedging requirements of the majority of ETH holders. This could potentially consolidate much of ETH options liquidity and volume into a single market.
Future Work
Future work lies primarily in the area of applications.
- Is there a market for everlasting options, or for other new funding-fee-based perpetuals?
- Which types will be most useful?
- How can they best be parameterized?
- How can exchanges and traders best manage their risk, and what are appropriate liquidation criteria for those trading on margin?
If you have thoughts about these questions, or questions of your own, we would love to hear from you.
You can email me at dave@paradigm.xyz or DM me on Twitter, or reach Sam at https://twitter.com/SBF_FTX.
PDF version: https://www.paradigm.xyz/static/everlasting_options.pdf
Acknowledgments: Dan Robinson for many conversations that contributed to this post, both indirectly and directly. Hasu for extensive feedback on clarity and structure for this paper. Georgios Konstantopoulos for suggesting appropriate graphs.
Disclaimer: This post is for general information purposes only. It does not constitute investment advice or a recommendation or solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. This post reflects the current opinions of the authors and is not made on behalf of Paradigm or its affiliates and does not necessarily reflect the opinions of Paradigm, its affiliates or individuals associated with Paradigm. The opinions reflected herein are subject to change without being updated.